一、运算封闭
若从某个非空数集中任选两个元素(同一元素可重复选出),选出的这两个元素通过某种(或几种)运算后的得数仍是该数集中的元素,那么,就说该集合对于这种(或几种)运算是封闭的。如自然数集N对加法,乘法运算是封闭的,整数集Z对加、减、乘法运算是封闭的,有理数集、复数集对四则运算是封闭的,初等函数集合对不定积分运算是不封闭的。
二、数域
数域简称域,设P是由一些复数组成的集合,其中包括0与1,如果P中任意两个数的和、差、积、商(除数不为0)仍是P中的数,则称P为一个数域,简称域。常见数域:复数域C;实数域R;有理数域Q。
注意:
-
任意数域P都包括有理数域Q,即有理数域为最小数域
-
设F1及F2是两个数域,则二者的交集也构成一个数域
-
自然数集N及整数集Z都不是数域
三、映射、陪域、值域
-
设X、Y是集合,若存在对应关系 使X中每个元素x在Y中有且仅有唯一元素y与之对应.则称 f 是从X到Y的映射,记作 f:X->Y。称元素y为元素x的象,元素x为元素y的象源,记作 f(x)=y。称集合X为映射f 的定义域,记作D(f) 或 dom(f)。称集合Y为映射f的陪域,记为C(f)或codom(f)。Y与X中元素有关系的元素集合{y|∃x(x∈X∧y=f(x)∈B)}称为映射的值域,记作 f(X)或V(X)或R(f)或 ran f。很显然,值域是陪域的子集;
-
上述定义中,定义域 X中的不同元素为值的x变元称为自变元或自变量;陪域 Y中的不同元素为值的y变元称为因变元或因变量
四、满射、单射和双射
4.1、定义
-
设f是从集合A到集合B的映射,若f(A)=B,即B中任一元素b都是A中某元素的像,即表示为:函数f: A → B为双射当且仅当对任意b∈B存在唯一a∈A满足f(a) = b。则称f为A到B上的满射;
-
设f是从集合A到集合B的映射,若对A中任意两个不同元素a1不等于a2,它们的像f1不等于f2,则称f为A到B的单射;
-
若映射f既是单射,又是满射,则称映射f为A到B的“双射”(或“一一映射”)。函数为双射当且仅当每个可能的像有且仅有一个变量与之对应。
4.2、补充说明
-
函数f : A → B为双射当且仅当其可逆,即存在函数g: B → A满足g ° f = A上的恒等函数,且f °g为B上的恒等函数,符号°表示函数复合运算。
-
若 X和 Y为有限集合,则存在两集合的双射函数当且仅当两个集合有相同的元素个数。
五、恒等函数
5.1、定义
恒等函数为一无任何作用的函数:它总是传回和其引数相同的值。换句话说,恒等函数为函数f(x) = x,输入等于输出。
定义:
设M为一集合,于M上的恒等函数f被定义于一具有定义域和陪域M的函数,其对任一M内的元素 x,会有f(x) = x 的关系。
于M 上的恒等函数f通常标记为: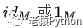
在一n 维向量空间内,不论其基为何,恒等函数表示成单位矩阵:
5.2、性质
设 f:M->N为任一函数,则会有:
其中" °"表示函数复合。
六、线性函数
在初等数学内,函数:f(x)=kx+b
该函数在平面直角坐标系中的图象是直线,所以称为线性函数,k称为斜率,b是f(x)在y轴上的截距,即函数图象与 y轴相交点的 y坐标。
改变斜率 k会使直线陡峭或平缓度发生变化,改变 截距b 会将直线上移或下移。
高等数学的线性函数是一个线性映射,将在后面的线性代数中介绍。
七、初等函数
初等函数是由幂函数(power function)、指数函数(exponential function)、对数函数(logarithmic function)、三角函数(trigonometric function)、反三角函数(inverse trigonometric function)与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方)及有限次函数复合所产生,并且能用一个解析式表示的函数。
初等函数在其定义区间内一定连续。
初等函数之外的函数都叫非初等函数。
八、小结
本文介绍了一些与函数相关的概念,包括运算封闭、数域、陪域、值域、满射、单射、双射、映射、恒等函数、初等函数等知识。
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/TTmFlHtJw9LVj3RdpKNiQw,如有侵权,请联系删除。










