人工智能数学基础9：集合相关概念 3年前

一、集合基础知识

• 集合的特性：

1. 确定性：给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现

2. 互异性：一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画，可以使用多重集，其中的元素允许出现多次

3. 无序性：一个集合中，每个元素的地位都是相同的，元素之间是无序的。集合上可以定义序关系，定义了序关系后，元素之间就可以按照序关系排序。但就集合本身的特性而言，元素之间没有必然的序

• 不包含任何元素称之为空集，记为∅，空集∅是任意一个非空集合的真子集，是任何一个集合的子集

• 补集又可分为相对补集和绝对补集

1. 相对补集定义：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或A\B，即A-B={x|x∈A，且x∉B} 。

2. 绝对补集定义：A关于全集合U的相对补集称作A的绝对补集，记作A’或∁u（A）或~A。有U’=Φ；Φ’=U

• 幂集：设有集合A，由集合A所有子集组成的集合，称为集合A的幂集，记作P(A) ，P(A)={x|x⊆A}。对于幂集有定理如下：有限集A的幂集的基数等于2的有限集A的基数次幂，即设集合A的元素个数|A|=n，则|P(A)|=2^n

• 全集：如果限定所讨论的集合都是某个集合的子集，则称该集合为全集，记作E，全集不唯一，如全集A是某个集合B的子集，则B一定也是全集

• 多重集：设全集为E，E中元素可以不止一次在A中出现的集合A称为多重集。若E中元素a在A中出现k次（k≥0），则称a在A中重复度为k，集合可看作重复度均小于等于1的多重集

• 偏序集与偏序关系：设P是集合，P上的二元关系“≤”满足以下三个条件，则称“≤”是P上的偏序关系（或部分序关系）：
  （1）自反性：a≤a，∀a∈P；
  （2）反对称性：∀a，b∈P，若a≤b且b≤a，则a=b；
  （3）传递性：∀a，b，c∈P，若a≤b且b≤c，则a≤c；
  具有偏序关系的集合P为偏序集（或称半序集），记为（P，≤）。a≤b读作“a小于或等于b”或“a含于b”，a<b读作“a小于b”或“a真含于b”。这里a<b等价于a≤b且a≠b，∀a，b∈P。若a≤b或b≤a，则称a与b是可比的，否则就说a与b是不可比。a与b不可比记作a||b。

• 偏序集逆关系及对偶：设（P，≤）是偏序集，对于P中任意二元x，y有:
  
  偏序集有如下定理：
  

• 全序集：也叫有序集，设(A，≤)是偏序集，如果(A，≤)中的关系“≤”满足条件：对于任意的a，b∈A，a≤b或b≤a至少有一个成立，那么就称关系≤为序关系，称A为在这个关系下的全序集

• 良序集：设集合(S,≤)为一全序集，≤是其全序关系，若对任意的S的非空子集，在其序下都有最小元素，则称≤为良序关系，(S,≤)为良序集。在数学中，集合S上的良序关系（或良序）需要满足：1.是在S上的全序关系 2.S的所有非空子集在这个次序下都存在最小元素(并非代数上的大小) 。集合S和这个良序关系一起就叫做良序集合。

• 模糊集：用来表达模糊性概念的集合，又称模糊集、模糊子集。普通的集合是指具有某种属性的对象的全体。这种属性所表达的概念应该是清晰的，界限分明的。因此每个对象对于集合的隶属关系也是明确的，非此即彼。但在人们的思维中还有着许多模糊的概念，例如年轻、很大、暖和、傍晚等，这些概念所描述的对象属性不能简单地用“是”或“否”来回答，而模糊集合就是指具有某个模糊概念所描述的属性的对象的全体。于概念本身不是清晰的、界限分明的，因而对象对集合的隶属关系也不是明确的、非此即彼的。这个概念我们知道即可，暂时用不着

• 如果两个集合S和T的元素完全相同，则称S与T两个集合相等，记为S=T ，即
  
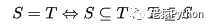
  其中双箭头符号称为当且仅当，表示左边的命题与右边的命题相互蕴含，即两个命题等价。

• [] 集合的表示方法通常有四种，即列举法 、描述法 、图像法 和符号法

1. 列举法就是将集合的元素逐一列举出来的方式,例如，光学中的三原色可以用集合{红，绿，蓝}表示、正整数集合{1,2,3，…,n,…}

2. 描述法：形式为{代表元素|满足的性质}，如正数表示{x：x∈R且x>0}。

3. 图像法，又称韦恩图法、韦氏图法，是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合，是集合的一种直观的图形表示法

4. 符号法：有些集合可以用一些特殊符号表示，举例如下：
   

二、对等集合与基数

对等集合：

两个能够建立元素间一一对应的集合称为互相对等集合。例如10台电脑的集合和10部手机的集合、奇数和偶数的集合。

基数：

基数（cardinal number）：简单来说集合中元素的数目称为集合的基数。在数学上，基数是集合论中刻画任意集合大小的一个概念。根据对等这种关系对集合进行分类，凡是互相对等的集合就划入同一类。这样，每一个集合都被划入了某一类。任意一个集合A所属的类就称为集合A的基数，记作|A|（或cardA)。这样，当A 与B同属一个类时，A与B 就有相同的基数，即|A|=|B|。而当 A与B不同属一个类时，它们的基数也不同。

如果把单元素集的基数记作1，两个元素的集合的基数记作2，等等，则任一个有限集的基数就与通常意义下的自然数一致 。空集的基数也记作0。于是有限集的基数也就是传统概念下的“个数”。但是，对于无穷集，传统概念没有个数，而按基数概念，无穷集也有基数，例如，任一可数集（也称可列集）与自然数集N有相同的基数，即所有可数集是等基数集。不但如此，还可以证明实数集R与可数集的基数不同。所以集合的基数是个数概念的推广。

基数的运算

基数可以比较大小。假设A，B的基数分别是a，β，即|A|=a，|B|=β，如果A与B的某个子集对等，就称 A 的基数不大于B的基数，记作a≤β，或β≥a。如果 a≤ β，但a≠β（ 即A与B不对等 ），就称A的基数小于B的基数，记作a<β，或β>a。

基数的三歧性定理——任何两个集合的基数都可以比较大小，即不存在集合A和B，使得A不能与B的任何子集对等，B也不能与A的任何子集对等。

基数可以进行运算 ，基数上的算术运算是对自然数运算的推广。

• 给定集合 X 与 Y，定义 X+Y={(x,0):x ∈ X} ∪ {(y,1):y ∈ Y}，则基数和是|X| + |Y| = |X + Y|。若 X 与 Y 不相交，则 |X| + |Y| = |X ∪ Y|。

• 基数积是|X||Y| = |X × Y|，其中 X × Y 是 X 和 Y 的笛卡儿积。

• 基数指数是|X|^|Y| = |X^Y|，其中 X^Y 是所有由 Y 到 X 的函数的集合。

在有限集时，这些运算与自然数无异。一般地：

• 加法和乘法是可交换的，即 |X|+|Y|=|Y|+|X| 及 |X||Y|=|Y||X|

• 加法和乘法符合结合律，即(|X|+|Y|)+|Z|=|X|+(|Y|+|Z|) 及 (|X||Y|)|Z|=|X|(|Y||Z|)

• 分配律，即 (|X|+|Y|)|Z|=|X||Z|+|Y||Z|| = |X||Y|+|X||Z|

无穷集合的加法及乘法非常简单。若 X 与 Y 皆非空而其中之一为无限集，则|X| + |Y| = |X||Y| = max{|X|, |Y|}

三、单位元

单位元也叫幺元（么元），是集合里的一种特别的元素，与该集合里的二元运算（类似于实数里的乘法*）有关。当单位元和其他元素结合时，并不会改变那些元素。

定义

设 (S,)为一带有一二元运算 的集合S（称之为原群），若S内存在一元素e:

• 如果对所有在S内的元素a而言，e*a=a，则e称为左单位元；

• 如果对所有在S内的元素a而言，a*e=a，则e称为右单位元；

• 若e同时为左单位元及右单位元，则称之为双边单位元，简称为单位元。

对应于加法的单位元称之为加法单位元（通常被标为0），而对应于乘法的单位元则称之为乘法单位元（通常被标为1）。

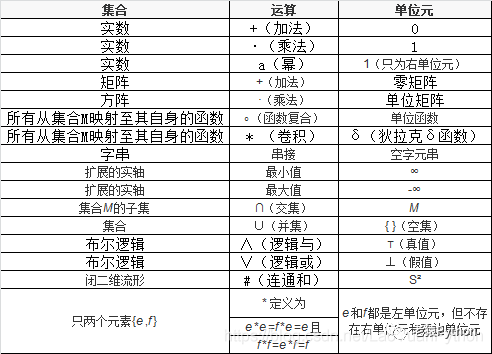
常见单位元

四、集合运算

集合的子交并补在此不介绍了，介绍一些其他的。本文下面资料参考百度文库，相关运算的描述应该是没有问题的，但相关运算符与一般看到的有比较大的差别，例如并集的运算符一般是∪而在此是[+]（也有些文档使用∨），交集的运算符一般是∩在此是[*]（也有些文档使用^），在此老猿会结合多个来源的资料将相关运算符都介绍一下。

• 和集：两个或两个以上集合的所有元素组成一个新集合，这个新集合称为和集。和集运算不剔除重复元素，这是和集与并集的区别。和集的运算符为[&]，如:
  （1,2,3）[&]（2,3,4）=(1,2,3,2,3,4)

• 对称差集：两个集合中非共同的元素的集合，运算符[/]或⊕，A⊕B=(A−B)∪(B−A)，如（1,2,3）[/]（2,3,4）=（1,4）

• 相对补集：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或A\B，即A-B={x|x∈A，且x∉B}

• 绝对补集：A关于全集合U的相对补集称作A的绝对补集，记作A'或∁u（A）、∁uA或~A

1. U'=Φ；Φ'=U

2. 根据绝对补集的∁uA记法，相对补集A-B还有一种记法：∁bA或∁b（A）

3. 绝对补集A'还有种记法：
   

• 双目运算符差集：第一个集合A减去第二个集合B所包含的元素，结果就是差集，也叫反交集，运算符为[-]，也有的记为-。差集的结果称为B对于A的补集或余集

• 单目运算符差集：去除集合中的重合元素，如(1,2,3,3,4)[-] = (1,2,3,4)

• 逆集：第二个集合减去第一个集合所包含的元素，也称为反差集，运算符[\]，如（1,2,3）[\]（2,3,4）=（4）

• 平集：两个集合的和集中，只出现一次的元素组成的集合称为平集，运算符[!]，如：（1,2,3,4）[!]（3,4,5,6）=（1,2,5,6）

• 频集：两个集合的和集中，出现两次以上的元素组成的集合称为频集，运算符为[!!]，如：（1,2,3,4）[!!]（3,4,5,6）=（3,4）`

• 求和：单目运算，求集合中所有元素的和，运算符[++]，可以放在集合前面也可以放在集合后面，如：(1,2,3)[++]=[++](1,2,3)=6

• 內积：单目运算，求集合或矩阵所有元素的乘积，运算符[**]，如[**](2,3,4,5)=120

• 算术平均值：单目运算，求集合中所有元素的算术平均值，运算符[~]，如[~](2,3,4,5)=3.5

• 标准方差：单目运算，集合或矩阵元素的方差的算术平方根，运算符[~~],可以在集合前或后，如：[~~][1,5,3;6,8,2;9,1,6]=2.9627,其中分号表示一行数据结束，下同

• n项移动平均：单目运算，集合元素的n项移动平均，运算符[~n],如：
  [~2](1,2,3,2,4,2,5)=1.5 2.5 3 3,3.5
[~3](1,2,3,2,4,2,5)=2 2.3333 2.6667 3.6667

• 方差：单目运算，集合或矩阵中各元素值与平均值的差的平方和的平均数，运算符号[~^]，如：
  ·（1,5,3,6,8,2,9,1,6）[~^]=8.7778`

• 频数表：单目运算，集合中每个元素出现的个数，运算符号[^]，有四种形式：

4. [^]或[^1]，按出现次数降序排列

5. [^2]按出现次数升序排列

6. [^3]按元素大小降序排列

7. [^4]按元素大小升序排列

• 矩阵求逆：单目运算，对集合中的元素按矩阵方式求逆，N阶矩阵A、B，如AB=1则称B是A的逆矩阵。矩阵求逆的运算符为[-1],如：
  （1,5,3;6,8,2;9,1,6）[-1]=-0.1901 0.1116 0.0579 0.0744 0.0868 0.0661

• 中值：也叫中间值，单目运算，对集合中的元素升序排列，处在中间的值称为中值，运算符号[|]，如：(1,2,3,2,4,2,5)[|] = 3

• 众数：也称典型值，单目运算，在集合中出现次数最多的元素及其次数，运算符号[||]，如：(1,2,2,3,4,4)[||]=2 2、4 2，表示2和4出现次数最多，都出现了2次

• 累加数列：单目运算，对集合中排列的元素逐个累加得到的数列，首个元素无需相加取自身的值作为结果，后面每个元素都与前面累加的结果相加得到当前项，运算符号[&+]，如：
  [&+](1,2,3,4,5)=1 3 6 10 15

• 累减数列：单目运算，数列中的元素后一个减前一个元素得到的数列，首个元素无需相减取自身的值作为结果，累加数列的逆运算，运算符号[&-]，如：
  [&-](1,3,6 ,10,15)=1,2,3,4,5

• 倒数数列：单目运算，集合中的每个元素求倒数组成的新集合，运算符号[&/]，如：
  [&/](1,2,4 ,10)=1,0.5,0.25,0.1

• 倒数和：单目运算，集合中的每个元素求倒数的和，运算符号[/+]，如：
  [&/](1,2,4 ,10)=1.85

• 几**何平均值：也叫级均值，单目运算，集合內积的开n次方,n为元素个数，运算符号[*~]，如：（1,2,4）[*~]=2

• 调和平均值：也叫谐均值，单目运算，集合所有元素倒数的平均数的倒数，运算符号[/~]，如：
  [/~](1,2,4 ,10)=2.162

• 最小值：单目运算，集合所有元素的最小值，运算符号[<]

• 最大值：单目运算，集合所有元素的最大值，运算符号[>]

• 降序排序：单目运算，集合所有元素进行降序排列，运算符号[>>]

• 升序排序：单目运算，集合所有元素进行升序排列，运算符号[<<]

• 反转：单目运算，集合所有元素倒序排列，运算符号[<>]

• 极差：单目运算，集合或矩阵最大数减最小数的值，运算符号[><]

• 转置：单目运算，对数列或矩阵进行转置，运算符号[T]，将矩阵的行变成列，列变成行

• 数据个数：单目运算，返回集合中元素个数，运算符号[N]

• 第n个元素值：单目运算，取出集合中第n个元素值，运算符号[n],其中n为具体序号（从1开始），如(1,2,3)[2]=2

• 第i行第j列值：单目运算，获得矩阵第i行第j列值，i、j从1开始计数，如：(1,2,3;4,5,6)[2,1]=4

• 行数：单目运算，获得矩阵的总行数，运算符[R]，如：(1,2,3;4,5,6)[R]=2

• 取出行：单目运算，获得矩阵的指定行数据，运算符[Rn],n为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1]=1 2 3

• 取出部分行：单目运算，获得矩阵的指定行数据，运算符[Ri,j],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6;7,8,9)[R1,2]=1 2 3;4,5,6

• 添加行：双目运算，将第二个矩阵加到第一个矩阵后面，运算符[+R]

• 添加1行：双目运算，将第二个矩阵的指定行加到第一个矩阵后面，运算符[+Ri]，i为具体行号，从1开始计数

• 单目运算行交换：将矩阵的第i行与第j行数据进行交换，运算符[Ri=Rj],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1=R2]=4,5,6;1 2 3

• 双目运算行替换：将矩阵1的第i行替换为矩阵2第j行数据，运算符[Ri=Rj],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1=R2]（7,8,9；0,2,4）=0,2,4；4,5,6

• 列数：单目运算，获得矩阵的列数，运算符[C]

• 取出矩阵的指定列：单目运算，获得矩阵指定列，运算符[Ci]，i为列号，从1开始计数

• 取出部分列：单目运算，获得矩阵部分列，运算符[Ci,j]，i、j为列号，从1开始计数

• 增加1列：双目运算，把第二个矩阵的指定列添加到第一个矩阵后面，运算符[+Ci],i为第二个矩阵列号，从1开始计数，如：(1,2,3;4,5,6)[+c1](7,8,9;0,2,4)=(1,2,3,7;4,5,6,0)

• 单目运列交换：将矩阵的第i列与第j列数据进行交换，运算符[Ci=Cj],i、j为具体列号，从1开始计数

• 双目运算行替换：将矩阵1的第i列替换为矩阵2第j列数据，运算符[Ci=Cj],i、j为具体列号，从1开始计数

五、集合运算定律

• 交换律：A∩B=B∩A；A∪B=B∪A

• 结合律：A∪(B∪C)=(A∪B)∪C；A∩(B∩C)=(A∩B)∩C

• 分配对偶律：A∩(B∪C)=(A∩B)∪(A∩C)；A∪(B∩C)=(A∪B)∩(A∪C)

• 同一律：A∪∅=A；A∩U=A

• 求补律：A∪A’=U；A∩A’=∅

• 对合律：A’’=A

• 等幂律：A∪A=A；A∩A=A

• 零一律：A∪U=U；A∩∅=∅

• 吸收律：A∪(A∩B)=A；A∩(A∪B)=A

• 反演律（德·摩根律）：(A∪B)’=A’∩B’；(A∩B)’=A’∪B’。文字表述：1.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集; 2.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集。
  注：有个集合的对偶律，老猿理解跟反演律是一回事，因此在此没有单列

• 容斥原理：

• card(A∪B)=card(A)+card(B)-card(A∩B)

• card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)

• 应用案例：
  问题：假设有100人参加了三个兴趣小组。其中参加数学兴趣小组的有55人，参加语文兴趣小组的有65人，参加英语兴趣小组的有70人，同时参加语文和数学兴趣小组的人数是31人，同时参加数学和英语兴趣小组的人数是40人，同时参加语文和英语兴趣小组的有25人，则三个兴趣小组都参加的人数是多少人?
  解答：(1) A+B+T=至少参与一项的总人数(无重叠)
  　　(2) A+2B+3T=至少参与一项的总人数(含重叠部分)
  　　(3) B+3T=至少参与两项的总人数(含重叠)
  　　(4) T三项都参与的人数。
  　　这里介绍一下A、B、T分别是什么：
  　　A=x+y+z;表示只参加一个兴趣小组的人数
  　　B=a+b+c;表示仅参加了两个兴趣兴趣小组的人数
  　　T=全部都参加的人数。
  　　通过公式有如下解法：
  　　(1) A+B+T=100;
  　　(2) A+2B+3T=55+65+70=190
  　　(3) B+3T=31+40+25=96
  　　实际上我们要求的是T， (1)+(3)-(2)=T。即得到答案T=100+96-190=6

六、小结

本文介绍了集合一些相关的基础概念、运算及定律，包括基数、对等集合、单位元以及类似补集、差集、对称差集等概念，这些知识对于阅读AI、线性代数等相关知识有一定的帮助。

参考文档：

百度百科

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》

本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/abeIQUs-aSQNMXwUN2Is_Q，如有侵权，请联系删除。