一、向量
1.1、向量定义
向量也称为欧几里得向量、几何向量、矢量,指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
-
在物理学和工程学中,几何向量更常被称为矢量。
-
一般印刷用黑体的小写英文字母(a、b、c等)来表示,手写用在a、b、c等字母上加一箭头(→)表示,如 :
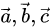
也可以用大写字母AB、CD上加一箭头(→)等表示。但由于输入法不支持,本文后面的向量表示就不输箭头,如直接叫向量a、b、c。
定义:
n个有顺序的数a1,a2,…,an组成的数组:
a=(a1,a2,…,an)
叫做n维向量,a1,a2,…,an叫做a的分量,ai叫做a的第i个分量。分量都是0的向量叫零向量。
两个向量相等当且仅当它们分量数量相同,且各分量都相等。
1.2、向量的模和范数
向量的模就是向量的大小,也就是向量的长度,表示符号为在向量两侧各加一竖线,如向量AB记作: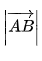
为了输入方便,以后老猿记为|向量AB|。
对于二维平面向量(x,y),其模长即为原点到该点的距离,大小为: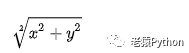
对于三维立体空间的向量(x,y,z),其模长为: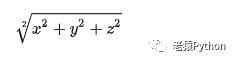
对于n维空间向量x(V1,V2,…,Vn),其模长为: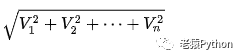
模是绝对值在二维和三维空间的推广,可以认为就是向量的长度。推广到高维空间中称为范数。
范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。
1.3、向量的属性及自由向量
-
向量规定了方向和大小,常用一条有向线段来表示,有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
-
长度相等且方向相同的向量叫做相等向量,向量a与b相等,记作a=b。零向量与零向量相等。
-
当用有向线段表示向量时,起点可以任意选取。任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关.同向且等长的有向线段都表示相同向量。
-
一个向量只要不改变它的大小和方向,它的起点和终点可以任意平行移动的向量,叫做自由向量。自由向量可以平移至空间任意点,这样一来,若已知向量的大小和方向,则向量就算给出。例如物体运动时的速度和加速度就是自由向量,在数学中把自由向量,简称为向量。数学中只研究自由向量。
-
因为方向不能比较大小,所以向量也就不能比较大小。对于向量来说“大于”和“小于”的概念是没有意义的。
1.4、单位向量
长度为一个单位(即模为1)的向量,叫做单位向量。与a同向,且长度为单位1的向量,叫做a方向上的单位向量。一个非零向量除以它的模,可得所需单位向量。记作: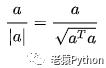
关于等式右边的含义,请参考下节关于向量点积的介绍:《https://blog.csdn.net/LaoYuanPython/article/details/112411742 人工智能数学基础-线性代数2:向量的点积、內积、数量积和外积》。
1.5、负向量
如果向量AB与向量CD的模相等且方向相反,那么我们把向量AB叫做向量CD的负向量,也称为相反向量。
1.6、零向量
长度为0的向量叫做零向量,记作0。零向量的始点和终点重合,所以零向量没有确定的方向,或说零向量的方向是任意的。
规定:所有的零向量都相等。
1.7、固定向量
固定向量也叫做胶着向量。在数学上指的是确定方向与大小、以及起点位置的向量。力学中的作用力就是固定向量。数学上不研究固定向量,只研究自由向量。
1.8、滑动向量
凡有大小及方向且需沿某一特定直线作用之向量,称之为滑动向量。
滑动向量的起点在空间内固定的一条直线上,而固定向量是起点位置固定,而自由向量则什么都没有固定。
1.9、位置向量
对于坐标平面(原点O)内的任意一点P,我们把向量OP叫做点P的位置向量,记作:向量P。
1.10、方向向量
方向向量(direction vector)是一个数学概念,空间直线的方向用一个与该直线平行的非零向量来表示,该向量称为这条直线的一个方向向量。
1.11、平行向量、共线向量
方向相同或相反的非零向量叫做平行(或共线)向量。向量a、b平行(共线),记作a∥b。零向量长度为零,是起点与终点重合的向量,其方向不确定。我们规定:零向量与任一向量平行。平行于同一直线的一组向量是共线向量。
1.12、 两向量共线
两平行向量 a与 b,可以平移至同一条与它们平行的直线上,故称此二向量a与b共线,也称向量a与b线性相关,否则,即 a不平行于b 时,称a与b线性无关。
1.13、共面向量
平行于同一平面的三个(或多于三个)向量叫做共面向量。
空间中的向量有且只有以下两种位置关系:⑴共面;⑵不共面。
注意:只有三个或三个以上向量才谈共面不共面。
1.14、法向量
法向量,是空间解析几何的一个概念,垂直于平面的直线所表示的向量为该平面的法向量。法向量适用于解析几何。由于空间内有无数个直线垂直于已知平面,因此一个平面都存在无数个法向量(包括两个单位法向量)。
二、向量的加减法
向量的加法、减法以及向量与数的乘法都称为向量的线性运算。
向量是将几何问题转化为代数问题的桥梁,向量的加减则是用代数方法进行几何运算。向量的加减法有几种方法。
2.1、分量加减法
向量的加减法就是对向量各个分量进行加减,假设有向量A(a1,a2,…,an)、向量B(b1,b2,…,bn),则:
`向量A+向量B = (a1+b1,a2+b2,...,an+bn) 向量A-向量B = (a1-b1,a2-b2,...,an-bn) ` * 1 * 2
2.2、头尾相接法(三角形定则)
对n维空间的向量A1、A2、…、An,各向量在n维空间表现为一原点到对应向量点的有向线段,起点为原点,终点为向量对应坐标点。当A1、A2、…、An各向量按顺序相加时,A1对应线段保持位置不变,其他向量对应线段的长度和方向保持不变,但将平移到其起点与前一向量线段的终点重合,如此将所有相加的向量首尾相接,最后构成的图形中,原点到最后一个向量终点的线段即为所有向量相加的结果。
如果是二维空间,则向量A1+向量A2+向量A3的过程及结果如下图左边: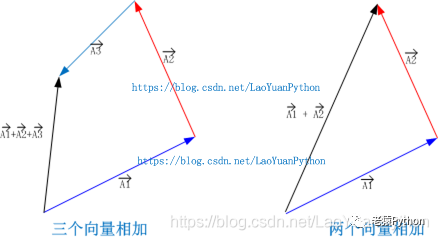
如果只有两个向量相加,则两个相加的向量和最终的结果向量构成一个三角形,如上图右边。因此这种方法又叫三角形定则。当超出三个的多个向量相加时,可以采用先将第一个和第二个向量相加得到的结果再与第三个向量相加,然后其结果再与第四个向量相加,…,以此类推,直到获得最后的结果。
以上方法,似乎只能用于求向量和,无法求向量差,其实向量减法也可以通过上述方法进行,将减去某个向量看成加上某个负向量,负向量与原向量的线段相同,只是箭头方向相反,即起点和终点相反,下图是 向量A1+向量A2 与 向量A1-向量A2 三角形定则法计算过程及结果图: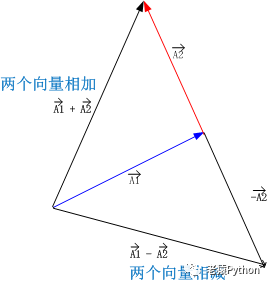
2.3、平行四边形定则
平行四边形定则只适用于两个非零非共线向量的加减。
平行四边形定则解决向量加法的方法:将两个向量平移至公共起点,以向量的两条边作平行四边形,结果为公共起点的对角线。下图为两个向量相加的三角形定则和平行四边形定则的对比,可以看到结果相同。
平行四边形定则解决向量减法的方法:将两个向量平移至公共起点,以向量的两条边作平行四边形,结果由减向量的终点指向被减向量的终点。下图为向量加减法的三角形定则法和平行四边形定则法的运算过程及结果对比: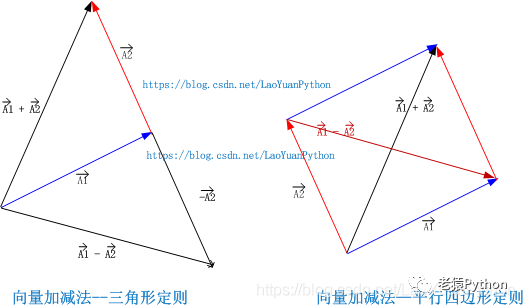
当将以上两个图中右边图形的线条改成虚线,将二者原点重合,可以得到如下图: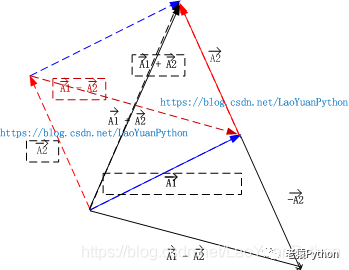
可以看到两种方法得到的加法结果向量完全重叠,而减法向量为平行四边形的对边,只是起点不同。
三、小结
本文介绍了向量的定义、向量的模、负向量、单位向量、零向量以及向量加减法的三种实现方法。
参考资料:
百度百科向量介绍
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/b6sZITDQ6zY7yzZbkar6pw,如有侵权,请联系删除。










