人工智能数学基础4：离差、平均差、方差、标准差、协方差、皮尔森相关系数 3年前

一、离差(Deviation)

离差即标志变动度，又称“偏差”，是观测值或估计量的平均值与真实值之间的差，是反映数据分布离散程度的量度之一，或说是反映统计总体中各单位标志值差别大小的程度或离差情况的指标，常写作：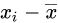

即参与计算平均数的变量值与平均数之差。离差的性质有二：(1)离差的代数和等于0；(2)参与计算平均数的各变量值与平均数之差的平均和，小于这些变量值与平均数之外的任何数之差的平均和。

二、平均差（Mean Deviation、Average Deviation）

平均差也称为均值，是数据分布中所有原始数据与平均数距离的绝对值的平均。平均差计算公式：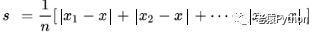

上述公式可以简记为：

其中，被减数代表每个数据的值，减数表示平均数，N=数据个数。

三、方差（Variance Deviation）

方差是各个数据与平均数之差的平方的和的平均数，即 ：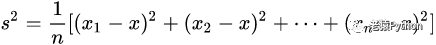
s²就表示方差。如果用作样本统计时，作为样本X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的(n-1)/n倍，因此用样本进行统计时，方差的计算公式调整为如下：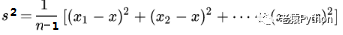

这就是统计上所谓的“无偏估计”。为了区分以上两种情况，第一个公式的结果称为总体方差，第二个公式的结果称为样本方差。

样本方差可以简记为：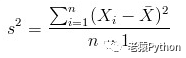

如果用D表示方差，则如下公式成立：

1. 设C是常数，则D（C）=0

2. 设X是随机变量，C是常数，则有：
   D(CX) = C²D(X)
   D(X+C) = D(X)

3. 设 X 与 Y 是两个随机变量，则有：
   D(X+Y) = D(X)+D(Y)+2cov(X,Y)
   D(X-Y) = D(X)+D(Y)-2cov(X,Y)
   D(aX+bY) = a²D(X)+b²D(Y)+2ab*cov(X,Y)
   其中cov表示协方差。

四、标准差（Standard Deviation）

对方差取算术平方根，得到的结果称为标准差，总体方差的算术平方根称为总体标准差，样本方差的算术平方根称为样本标准差。

样本标准差可以简记为：

五、协方差（Covariance）

离差、平均差、方差、标准差一般是用来描述一维数据的，但实际中常常遇到含有多维数据的数据集，如果需要评估两个数据之间的联系，可以使用协方差。协方差是一种用来度量两个随机变量关系的统计量，其计算公式如下：

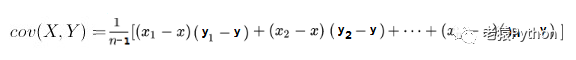
也可以记为：

可以看出，方差是协方差在X=Y时的一种特例。

协方差的结果如果为正值，则说明两者是正相关的，如果结果为负值就说明负相关的，如果为0，也是就是统计上说的“相互独立”。

从协方差的定义上我们也可以看出一些显而易见的性质，如：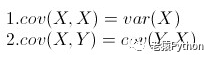

六、协方差矩阵（covariance matrix）

协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算 n! / ((n-2)!*2) 个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。

在统计学与概率论中，协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广。

协方差矩阵定义：
设X=（x1,x2,…,xn）为n维变量，则称矩阵：

为n维随机变量 的协方差矩阵（covariance matrix），也记为 D(X)，其中：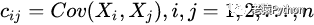

为X的分量Xi 和 Xj的协方差。

协方差矩阵为对称非负定矩阵，协方差矩阵具有如下性质：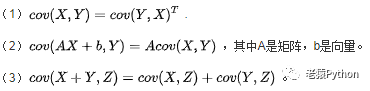

公式中右上角的T表示矩阵的转置矩阵，转置是一个数学名词，即矩阵的行和列对应互换。直观来看，将矩阵A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转，即得到A的转置。一个矩阵M, 把它的第一行变成第一列，第二行变成第二列，…,最末一行变为最末一列， 从而得到一个新的矩阵N。

七、皮尔森相关系数(Pearson correlation coefficient)

7.1、概述

皮尔森相关系数也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ，是一种线性相关系数，是最常用的一种相关系数。皮尔森相关系数记为r，用来反映两个变量X和Y的线性相关程度，r值介于-1到1之间，绝对值越大表明相关性越强。

7.2、定义

皮尔森相关系数为两个变量X、Y之间的协方差和两者标准差乘积的比值。定义公式如下：
r=ρ(X,Y)=cov(X,Y)/(σ(X)*σ(Y))
σ表示标准差。

由于方差是协方差的特例，标准差又是方差的算术平方根，因此上述公式也可以这样表示：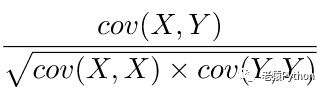

7.3、值含义

相关系数的绝对值越大，相关性越强：相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

当r大于0小于1时表示x和y正相关关系。当r大于-1小于0时表示x和y负相关关系。当r=1时表示x和y完全正相关，r=-1表示x和y完全负相关。当r=0时表示x和y不相关

通常情况下通过以下取值范围判断变量的相关强度：

• 0.8-1.0 极强相关

• 0.6-0.8 强相关

• 0.4-0.6 中等程度相关

• 0.2-0.4 弱相关

• 0.0-0.2 极弱相关或无相关

参考资料：

1. 百度百科；

2. 皮尔森相关系数(Pearson correlation coefficient)

本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/EjOBKMkCVX3Y51zJDOorVw，如有侵权，请联系删除。