4.1 手写Java PriorityQueue 核心源码 4年前

本章先讲解优先级队列和二叉堆的结构。下一篇代码实现

从一个需求开始

假设有这样一个需求：在一个子线程中，不停的从一个队列中取出一个任务，执行这个任务,直到这个任务处理完毕，再取出下一个任务，再执行。

其实和 Android 的 Handler 机制中的 Looper 不停的从 MessageQueue 中取出一个消息然后处理是一样的。

不过这个需求还有一点。需要我们的任务是有优先之分的，优先高的先执行，优先级低的后执行。比如现在队列中已经有了10个任务了，现在有一个紧急的任务需要处理，怎么办？

解决办法有多种：

1. 用数组实现，把任务放到数组里面，每次任务入队后，根据任务的优先级排序，把优先级最大的排到最前面，取任务的时候从队头取
2. 用链表实现，每次入队的时候把每个元素的优先级比较一下，把优先级最大的放链表尾部，取的尾部，取任务的时候每次都从尾部取就行了。

总结：上面两种方法都可以实现，不过都有一定的缺点

• 第一种方法，用数组实现，入队的时候，需要遍历整个数组，才能找到合适的位置

入队的时间复杂度是O(n),出队的时间复杂度是O(1)

• 第二种方法，用链表实现，和数组一样，也是需要遍历整个链表，才能找到合适的位置，入队的时间复杂度是O(n),出队的时间复杂度是O(1)

虽然出队效率很高，但是入队效率太低。有没有一种方法入队出队效率都很高呢？ 当然有，就是Java 给我们提供了一个 PriorityQueue 也就是优先级队列 我们来看一下PriorityQueue的用法

PriorityQueue的用法

我们有一个任务类，在里面执行一些操作。如下：

copy
/**
 *  我们的任务类
 */
public class Task {
    //任务的名称
    public String name;

    //优先级，是一个整数，我们规定，数越大优先级越高
    public int priority;


    public Task(String name,int priority){
        this.name = name;
        this.priority = priority;
    }

    //假如这是任务需要做的事
    public void doSomthing(){
        System.out.println("do somthing");
    }

    @Override
    public String toString() {
        return "taskName=" + name + " taskPriority=" + priority;
    }
}

测试代码如下：

copy
public static void main(String[] args){

        //比较两个任务，从大到小排序
        Comparator<Task> comparator = new Comparator<Task>() {
            @Override
            public int compare(Task o1, Task o2) {
                if(o1.priority > o2.priority){
                    return -1;
                }else if(o1.priority == o2.priority){
                    return 0;
                }else {
                    return 1;
                }
            }
        };

        //新建一个任务
        Queue<Task> priorityQueue =  new PriorityQueue<Task>(10,comparator);

        //新建了4个不同优先级的任务入队，数越大优先级越大，也最先执行
        priorityQueue.add(new Task("task1",23));
        priorityQueue.add(new Task("task2",34));
        priorityQueue.add(new Task("task3",15));
        priorityQueue.add(new Task("task4",79));

        //分别取出任务，然后打印
        System.out.println(priorityQueue.poll());   // 首先应该是 task4， 先取出来，因为优先级最大
        System.out.println(priorityQueue.poll());   // 然后才是   task2   被取出来
        System.out.println(priorityQueue.poll());   // 然后才是   task1   被取出来
        System.out.println(priorityQueue.poll());   // 最后才是   task3   被取出来，因为优先级最小
    }

输出如下：

copy
taskName=task4 taskPriority=79
taskName=task2 taskPriority=34
taskName=task1 taskPriority=23
taskName=task3 taskPriority=15

由此可知，虽然入队的顺序是不一样的，但是出队的顺序，是优先大的先出队 如果现在有一个紧急的任务需要优先处理，那么就可以设置这个任务的优先级比79大， 就可以排到最前面，等到下一次从队列中取任务的时候，这个紧急的任务就被取出来了。

这就是优先级队列的作用。

PriorityQueue队列的原理

直接上结论：

1. PriorityQueue是一个最大堆（或者用最小堆也是一样）
2. 堆一种完全二叉树
3. PriorityQueue是用一个数组存放二叉树中的元素的。

1 什么是完全二叉树？

完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1 ～ h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

定义太抽象，我们上图来描述什么是二叉树。

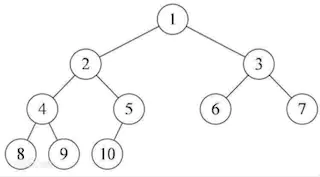
上由图可知：二叉树节点节点都在最左边。这就是完全二叉树，形态要记牢哦。

2 什么是堆结构？

堆结构有最大堆和最小堆，这里我们以最大堆为例。（最大堆懂了，那么最小堆自然就懂了）。 最大堆定义： 最大堆是一个完全二叉树，并且根节点的数都比左右两个节点的数大。

说白了就是最大的节点作用根。 由定义可知，最大堆有 2 个性质

1. 最大堆是一个完全二叉树
2. 最大堆，根节点比左右两个子节点大

如下图，是一个最大堆：

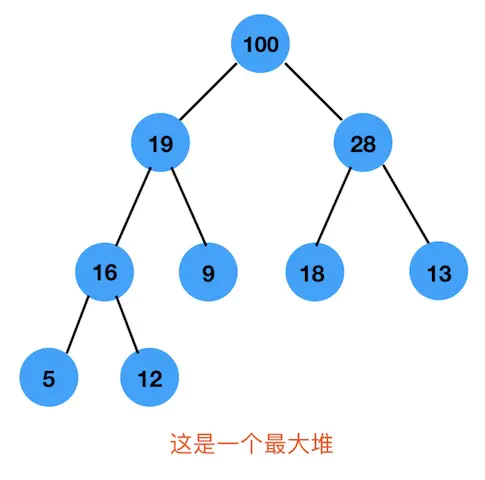
上图是一个最大堆，首先是一棵完全二叉树，并且每个根节点都大于它的左右子节点

这就是最大堆结构，当然最小堆和最大堆是反着的，根节点比左右子节点要小。 最大堆的形态要记牢哦。

最大堆和优先级队列

由上图最大堆可知：

1. 假如取元素的时候，只取整棵树的根节点，也就是 100 那个节点。也就是优先级最高的节点。
2. 100 节点取走以后，我们只需要把剩下的节点中，找个最大的，放在根节点位置，
3. 插入一个节点的时候，我们保证插入的节点放在适合的位置，满足二叉堆的性质即可。

那么这样的数据结构不就是优先级队列吗。 现在的问题就是

1. 如何用数组来存放二叉堆结构？（上面说了，二叉堆是用数组来存放数据的）
2. 如何向二叉堆中插入一个节点，并放到合适的位置上?
3. 取出根节点后，怎么找到剩下的最大的节点并放到合适的位置上？

下面我们来一一解决上面三个问题

1 如何用数组来存放二叉堆结构？

我们以下图一个简单的二叉堆为例

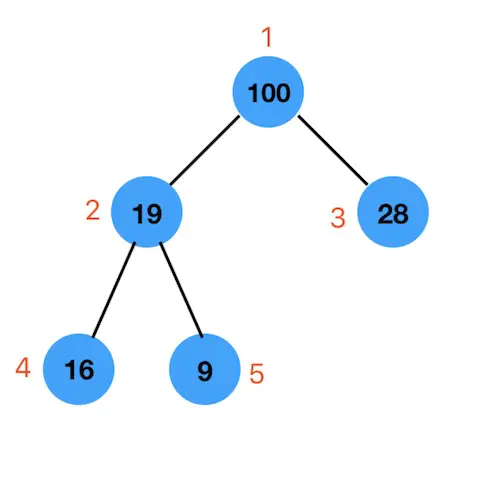
我们从左往右，按层序遍历，分别存放到数组的相应索引对应的位置上。 数组的第0个索引位置我们不用，从索引为1的位置开始存放。 最终这个最大堆存放到数组中，如下图

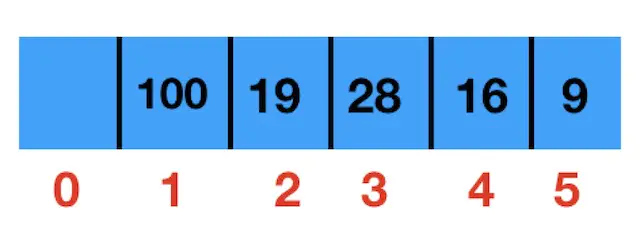
索引为0的位置不用。从1开始，为了方便后面计算。

对照图这两副图可以知道，二叉堆中的元素分层存放到数组中（从索引1开始存放） 有下面几个性质： 1 对于一个索引为n的节点，它的左孩子的索引是 2*n ,它的右孩子索引是2*n+1

比如 索引为2的节点是19

1. 那么它的左孩子是 2 * 2 是数组中的索引为4的位置 ，也就是16
2. 它的右孩子是 2*2 + 1 是数组中的索引为5的位置，也就是9

同样也可以由节点的索引，知道此节点的父节点的索引。 比如 索引为2的节点是19 那么它的父节点是 2 / 2 ，也就是索引为1的位置 比如 索引为3的节点是28 那么它的父节点是 3 / 2 ，也是 1 ，是和图中能对得上吧。

由此可知：用数组存放二叉堆（从索引为1开始），有以下两个性质： 对于索引为 n 的节点

1. 找孩子节点：左孩子的索引是 2*n ,右孩子的索引是 2*n + 1
2. 找父节点： 父节点的索引是 n/2

注：只有完全二叉树按层序存放到数组中才有这样的性质。必须是完全二叉树，必须是完全二叉树，必须是完全二叉树。重要的事情说三遍

2 如何向二叉堆中插入一个节点，并放到合适的位置上?

要向二叉堆中插入一个节点，插入节点后 只需要满足是完全二叉树并且任意一个根节点都比它的左右两个孩子的大就行了。

感觉说的是废话 如下图，我们要向二叉堆中插入一个节点为 30 的元素。

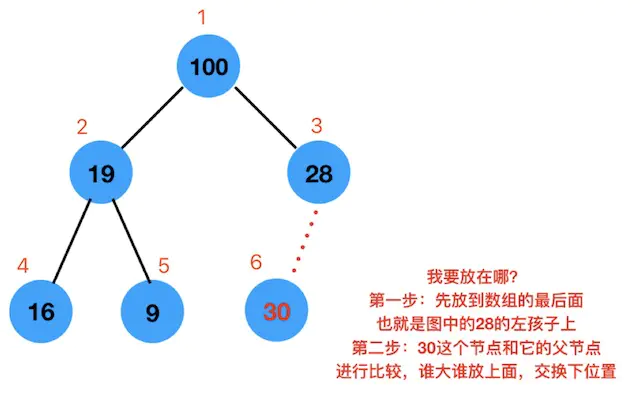
1. 第一步：新来的节点放到数组的最后的位置 也就是索引为 6 的位置（数组大小不够了就扩容，后面讲）
2. 第二步：不停的与自己的父节点比大小，比父节点大，就交换位置 然后重复以上步骤

经过上面两步，就可以将一个节点插入到合适的位置上了。如下图

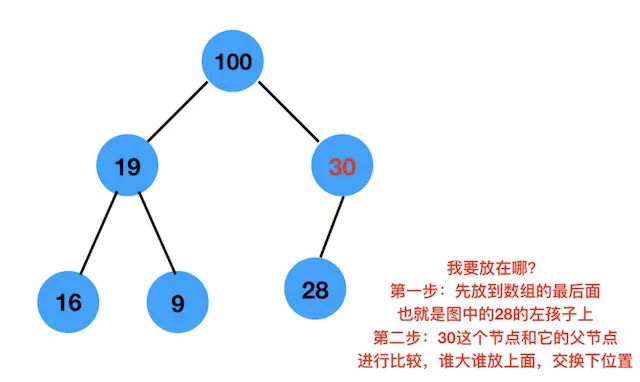
知道了如何向二叉堆中插入一个节点，，那么如何取出根节点后，怎么找到剩下的最大的节点并放到合适的位置上？也就是删除根节点后，剩下的怎么办呢？

3 如何删除根节点？

删除根节点很容易，关键是删除后剩下的节点怎么摆放？如下图

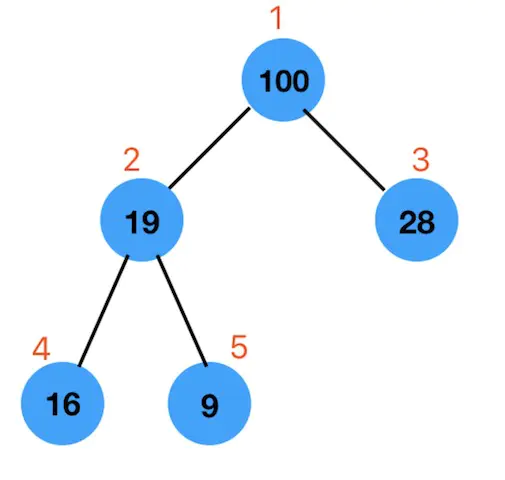
把根节点100删除后

1. 第一步：把最后一个节点9放到100的位置上，也就是索引为 1 的位置上。
2. 第二步：从根节点开始，不停的与它的左右两上节点比大小，找到左右两个节点为中的比较大的节点，然后交换位置，以此类推，直到这个节点比它的左右两个节点都大为止

如下图，第一步：

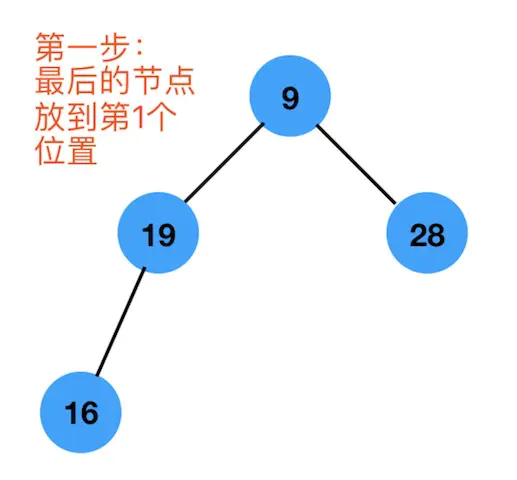
第二步：找出根节点9的最大的孩子节点 ，也就是 28，然后交换位置 ：如下图

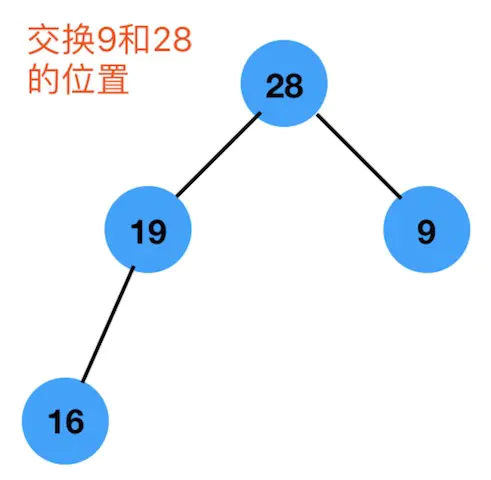
直到没有孩子可以比较了或者说有孩子，但是比孩子的节点要大，便不再比较

由上面可以知道，插入和删除都有了，下一章节就是代码实现了