一、三角函数的定义及名称
在直角三角形中,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个直角三角形,其中∠ACB为直角。对∠BAC(在此简称为θ)而言,对边(opposite)a=BC、斜边(hypotenuse)c=AB、邻边(adjacent)b=AC,则三角函数定义如下:
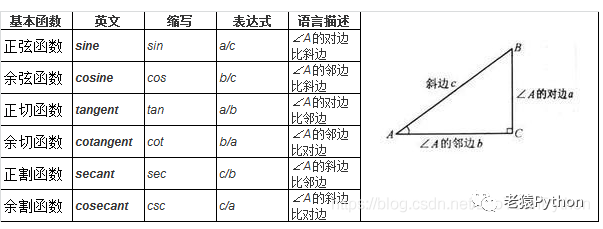
二、三角函数的变化趋势及图像
-
正弦值在 [2kπ-π/2,2kπ+π/2](k为实数,下同)随角度增大(减小)而增大(减小),在 [2kπ+π/2,2kπ+π*3/2] 随角度增大(减小)而减小(增大)
-
余弦值在 [2kπ-π,2kπ] 随角度增大(减小)而增大(减小),在 [2kπ,2kπ+π]随角度增大(减小)而减小(增大)
-
正切值在 [kπ-π/2,kπ+π/2] 随角度增大(减小)而增大(减小)
-
余切值在 [kπ,(k+1)π] 随角度增大(减小)而减小(增大)
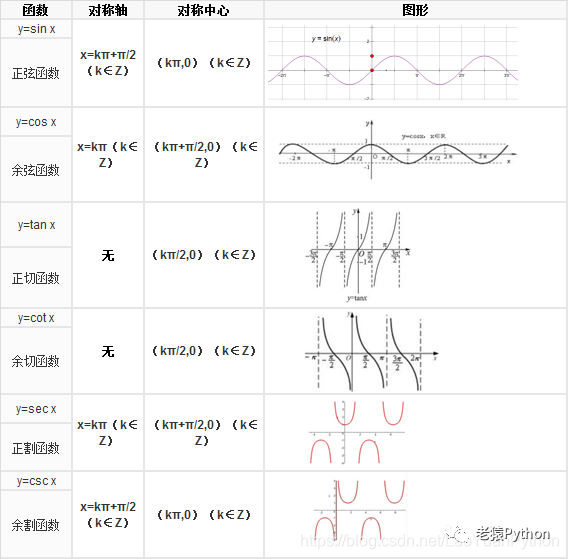
三、三角函数诱导公式
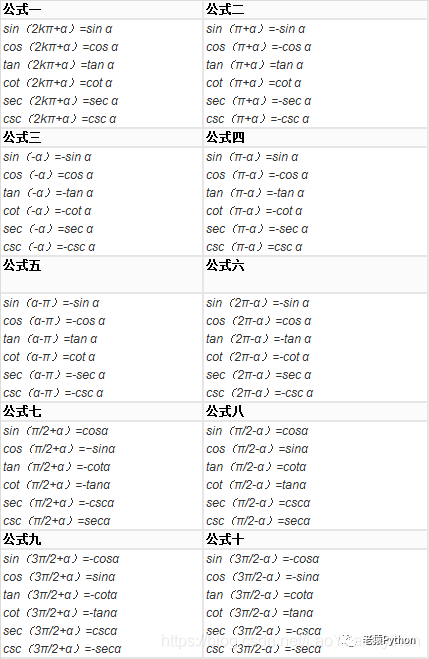
四、三角函数公式
4.1、三角函数之间的关系

4.2、三角恒等式
4.2.1、两角和与差
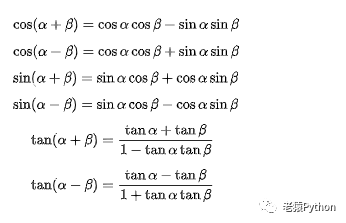
4.2.2、和差化积
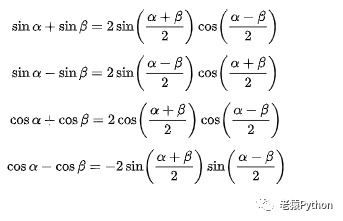
4.2.3、积化和差
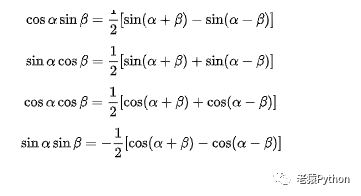
4.2.4、二倍角公式
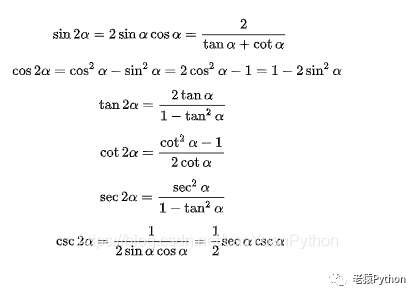
4.2.5、三倍角公式
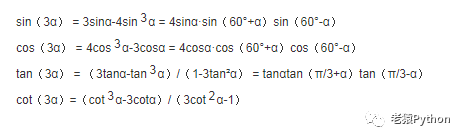
4.2.6、n倍角公式
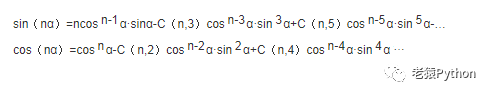
4.2.7、半角公式
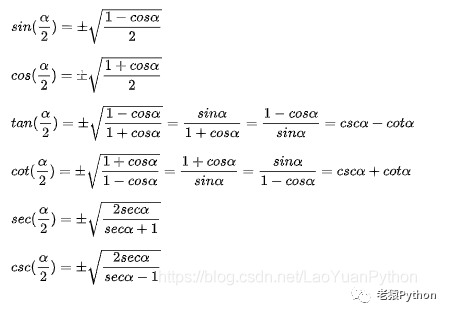
4.2.8、辅助角公式
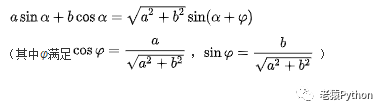
4.2.9、万能公式

4.2.10、降幂公式
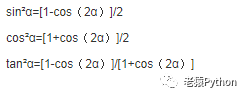
4.2.11、三角和
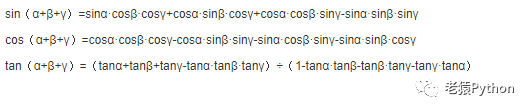
4.2.12、正弦定理
-
对于边长为a,b和c而相应角为A,B和C的三角形,有:sinA / a = sinB / b = sinC/c,可表示为:a/sinA=b/sinB=c/sinC=2R
-
变形:a=2RsinA,b=2RsinB,c=2RsinC,其中R是三角形的外接圆半径
-
三角形的面积:S=1/2absinC=1/2bcsinA=1/2acsinB
4.2.13、余弦定理
对于边长为a、b、c而相应角为A、B、C的三角形,有:
a² = b² + c²- 2bc·cosA
b² = a² + c² - 2ac·cosB
c² = a² + b² - 2ab·cosC
也可表示为:
cosC=(a² +b² -c²)/ 2ab
cosB=(a² +c² -b²)/ 2ac
cosA=(c² +b² -a²)/ 2bc
延伸定理:第一余弦定理(任意三角形射影定理)
a=b·cos C+c·cos B, b=c·cos A+a·cos C, c=a·cos B+b·cos A
4.2.14、正切定理
对于边长为a,b和c而相应角为A,B和C的三角形,有:
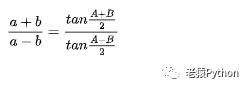
4.2.15、正切恒等式
对于任意非直角三角形中,如三角形ABC,总有:
tanA+tanB+tanC=tanAtanBtanC
五、三角函数固定角常量值
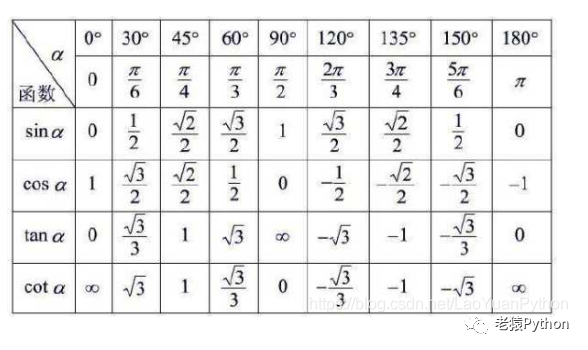
六、反三角函数
1、定义
反三角函数是一种基本初等函数。它是反正弦arcsin x,反余弦arccos x,反正切arctan x,反余切arccot x,反正割arcsec x,反余割arccsc x这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切 ,反正割,反余割为x的角。
由于基本三角函数具有周期性,所以反三角函数是多值函数,并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数 y=x 对称。
为限制反三角函数为单值函数,将反正弦函数的值y限在-π/2≤y≤π/2,将y作为反正弦函数的主值,记为y=arcsin x;相应地,反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2<y<π/2;反余切函数y=arccot x的主值限在0<y<π。
2、相关公式
余角关系
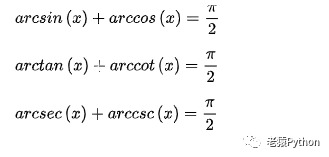
负数关系

倒数关系

加减法公式
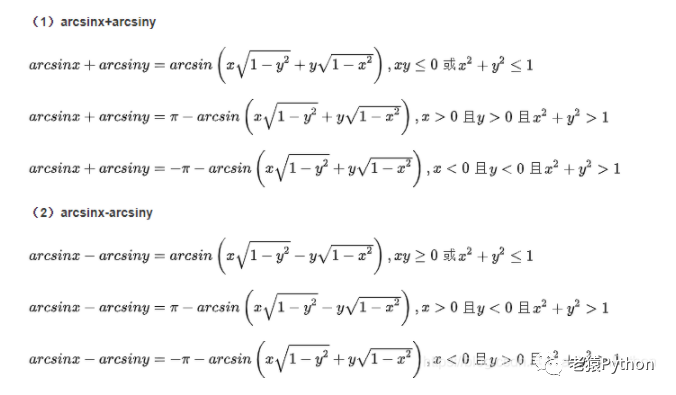
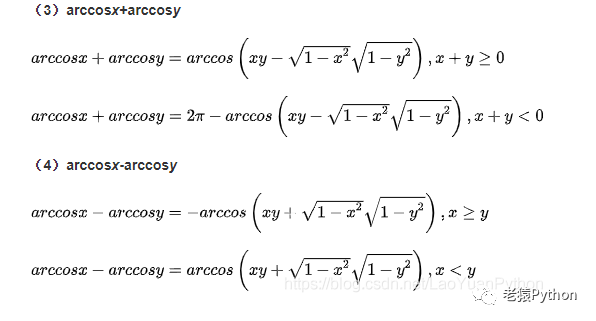

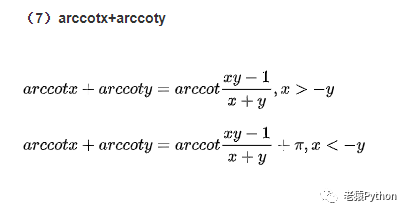
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/7Qg7MOo_N4_tjV9radXkCw,如有侵权,请联系删除。










