人工智能数学基础-线性代数4：矩阵及矩阵运算 3年前

一、矩阵定义

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，定义如下：
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

对于一个m×n 的矩阵A中某行的所有n个元素组成的n维向量叫做A的行向量，由A中某列的所有m个元素组成的m维向量叫做A的列向量。

A中的第i个行向量横写成：(ai1…ain)
第j个列向量竖写成：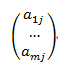

有时为了方便也横写。

只有一行一列的矩阵通常也可以叫做向量。

二、矩阵的秩

2.1、定义

一个矩阵,它的列矢量的极大无关组中矢量的个数叫做列秩,行矢量的极大无关组中矢量的个数叫做行秩,而它最大的且不等于0的子行列式的阶数r叫做它的秩。

可以证明,矩阵的行秩等于列秩等于秩,对于m×n矩阵而言,若 r=min(m,n) ,则称之为满秩矩阵，否则就叫降秩矩阵。矩阵A的秩用秩A表示，也可以用rank A表示。

对n阶方阵A,若rank A=n,则称A为非奇异矩阵（nonsingular matrix），否则称为奇异矩阵（singular matrix）。奇异矩阵对应行列式为0。可逆方阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。

2.2、关于矩阵秩的定理和属性

2.2.1、几个定理

1. 定理1：（m,n）-矩阵A的m个行向量线性相关的充要条件是A的秩小于m；

2. 定理2：（m,n）-矩阵A的秩等于r的充要条件是A中有r个行（列）向量线性无关，并且任意r+1个行（列）向量都线性相关；

3. 定理3：假定a1,…,an是n个向量，β1…βm都是a1,…,an的线性组合。如果m>n，那么β1…βn线性相关。

4. 定理4：假如矩阵A经过若干个行初等变换（如互换两行、用一个不为0的数乘某行、或者某行加到另一行等）变为矩阵B，那么A、B的秩相等

5. 定理5：满秩矩阵用行初等变换可以变为单位矩阵。

2.2.2、矩阵初等变换

互换矩阵的两行、用一个不为零的数乘A的一行以及用一个数乘A的一行加到另一行上，这些变换叫做A的行初等变换。类似的，还有矩阵的列初等变换。二者统称为矩阵A的初等变换。

假如矩阵A经过若干个行初等变换变为矩阵B，则A和B的秩相等。

三、矩阵的运算

矩阵的基本运算包括矩阵的加法、减法、数乘、乘法、转置。

3.1、矩阵的加减法

矩阵的加减法是两个同型矩阵（行数、列数相同）之间的加减法，两个m×n矩阵A和B的和，标记为A+B，差记为A-B，对应结果都是m×n矩阵，其内的各元素为A、B各相同位置元素进行加减后的值。

矩阵加法满足交换律和结合律：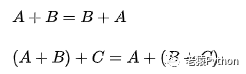

3.2、矩阵的数乘

3.2.1、定义

矩阵的k倍数乘，是以一个实数k与矩阵A相乘，其结果B是与A同型矩阵，B的每个元素都是A相同位置元素乘以k的结果。矩阵数乘本质上是在矩阵的每个元素上乘了一个k，用向量的数乘来解释，即是对每个行向量乘了k, 或者也相当于对每个列向量乘了k。

3.2.2、矩阵数乘运算定律

设A、B为矩阵，m、n为实数，则：

• （mn）A=m(nA)

• (m+n)A =mA + nA

• m(A+B) = mA + mB

矩阵的加减法和数乘运算称为矩阵的线性运算。

3.3、矩阵乘法

3.3.1、乘法定义

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。
设A为 m×p的矩阵，B为p×n 的矩阵，那么称m×n 的矩阵C为矩阵A与B的乘积，记作 C=AB，其中矩阵C中的第i行第j列元素等于矩阵A的第i行的元素与矩阵B的第j列对应元素乘积之和。可以表示为：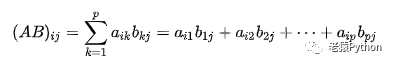

矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
如：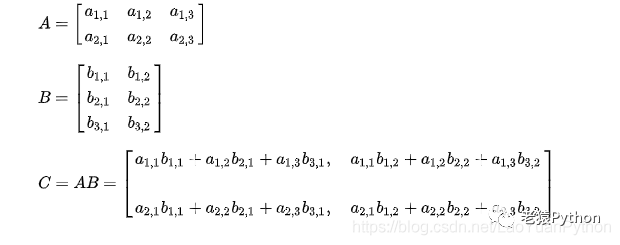

3.3.2、乘法定律

• 乘法结合律：(AB)C=A(BC)

• 乘法左分配律：(A+B)C=AC+BC

• 乘法右分配律：C(A+B)=CA+CB

• 对数乘的结合性k(AB）=(kA)B=A(kB）

• 转置 (AB)T=BTAT

另外矩阵乘法在以下两种情况下满足交换律：

• AA*=A*A，A和伴随矩阵相乘满足交换律

• AE=EA，A和单位矩阵或数量矩阵满足交换律。

更多矩阵乘法的介绍请参考《百度百科关于矩阵乘法的介绍》。

3.4、矩阵转置

设A为m×n阶矩阵（即m行n列），第i 行j 列的元素是a(i,j)，即：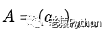

把m×n矩阵A的行换成同序数的列得到一个n×m矩阵，此矩阵叫做A的转置矩阵，记做AT或A’
例如矩阵: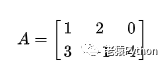

的转置矩阵为：

矩阵与其转置矩阵的秩相等。

矩阵的转置且满足下列运算运算定律：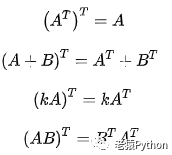

矩阵乘法的更多介绍请参考《百度百科矩阵乘法介绍》。

3.5、关于矩阵运算的有关补充

• 矩阵A+B的秩小于A的秩+B的秩

• 矩阵A、B的乘积的秩不大于A的秩与B的秩

• |kA| = kn|A|

• 对于n阶方阵A，存在正整数k，使得Ak=0，这样的方阵N就叫做幂零矩阵。满足条件的最小的正整数k被称为N的度数或指数

• 两个满秩矩阵的乘积仍是满秩矩阵

• 两个n阶方阵A、B的乘积AB的行列式等于A的行列式乘B的行列式，即|AB|=|A|×|B|

• 矩阵A、B的乘积的转置矩阵(AB)‘等于B的转置矩阵B’和A的转置矩阵A’的乘积，即：(AB)’=B’A’

四、部分特殊矩阵

4.1、单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵，记为 In或 En，通常用I或E来表示。

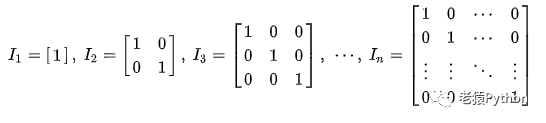
4.2、逆矩阵和伴随矩阵

4.2.1、逆矩阵定义

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得：AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵，记为：
A = B-1 B = A-1

4.2.2、逆矩阵性质

• A与B的地位是平等的，故A、B两矩阵互为逆矩阵，也称A是B的逆矩阵

• 单位矩阵的逆矩阵是它本身

• 零矩阵是不可逆的，即取不到B，使OB=BO=E

• 如果A可逆，那么A的逆矩阵是唯一的

• 若A可逆,则AT亦可逆,且(AT)-1=(A-1)T

• 若A、B为同阶方阵且均可逆，则AB亦可逆,且(AB)-1=B-1 A-1

• 矩阵A是可逆矩阵的充要条件是A为满秩矩阵

• |A-1|=|A|-1

4.3、对角形矩阵和数量矩阵

除主对角线上的元外其他元都是0的n阶方阵称为对角形矩阵。

数量矩阵就是对角线上元素都是同一个数值，其余元素都是零。
设E是单位矩阵, k是任何实数,则kE就是数量矩阵（数乘运算请参考下面矩阵运算部分的介绍）。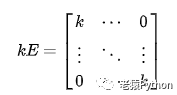

4.2.3、伴随矩阵定义

设A是一个n阶方阵，A=(aij)n×n，在行列式的章节中我们介绍过，将矩阵A 的元素aij 所在的第i行第j列元素划去后，剩余的各元素按原来的排列顺序组成的n-1阶矩阵所确定的行列式为元素 aij的余子式，记为 Mij，其对应的代数余子式：
Aij=（-1）i+jMij。

方阵A 的各元素的代数余子式Aij 所构成的如下矩阵 A*：

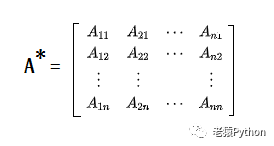
该矩阵 A*称为矩阵 A的伴随矩阵。

4.2.3、伴随矩阵性质

• 如果 A可逆，则 A*=|A|A-1

• |A*| = |A|n-1

• (kA)* = kn-1A *

• 若A可逆，则(A-1)* = (A*)-1

• (AT)* = (A*)T

• • [ ] (AB)* = B* A*,实际上该公式可以扩展到多个矩阵的情况，多个矩阵的乘积的伴随矩阵等于这些矩阵的伴随矩阵逆序的乘积

• AA* = A* A=|A|E
  从该公式可以看出，矩阵A如果是可逆矩阵，则：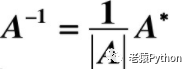
  

4.4、三角形矩阵

主对角线以下或以上的全体元素都是零的n阶方阵称为三角形矩阵。形如：

主对角线以上的全体元素都是零的n阶方阵称为上三角形矩阵，亦称上三角矩阵。

主对角线以下的全体元素都是零的n阶方阵称为下三角形矩阵，亦称下三角矩阵。

上三角形矩阵和下三角形矩阵统称三角形矩阵。

主对角元全是1的三角形矩阵称为特殊三角形矩阵。

主对角元全为零的三角形矩阵称为严格三角形矩阵。

两个n阶上(下)三角形矩阵的和、积以仍是上(下)三角形矩阵。

4.5、分块矩阵

4.5.1、定义

将一个矩阵用若干条横线和竖线分成许多个小矩阵，将每个小矩阵称为这个矩阵的子块，以子块为元素的形式上的矩阵称为分块矩阵。

4.5.2、运算规则

对于乘法来说进一步解释如下：


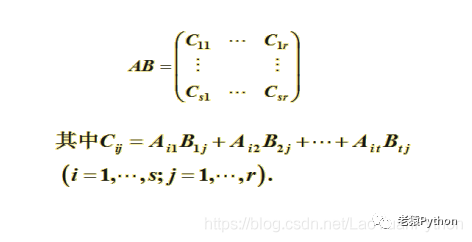
老猿总结：

分块矩阵加减法、数乘、转置、乘法的运算，可以将分块的子矩阵看做矩阵的元素，其运算规则与矩阵元素运算规则相同。但乘法要注意分块合适，且相关运算符合乘法的要求，即被乘数矩阵的列等于乘数矩阵的行数。

4.6、分块对角矩阵

4.6.1、定义

分块对角矩阵是一种特殊的分块矩阵，设A为n阶方阵，若A的分块矩阵在非主对角线上的子块皆为零矩阵，且在主对角线上的子块都是方阵，即：

其中O表示零矩阵， Ai(i=1,2,…,s)都是方阵，那么称A为分块对角矩阵，该形状称为分块对角形。

4.6.2、性质

针对上述分块对角矩阵，有如下性质：

• |A| = |A1| |A2|… |AS|

• 如果Ai≠0(i=1,2,…,s)，则A可逆，且：
  

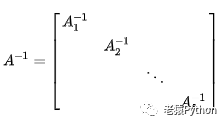
• 同结构的准对角矩阵的和、差、积、数乘及逆仍是准对角矩阵，且运算表现为对应子块的运算

4.7、矩阵的标准形

一个矩阵只有前面某些第i行、第i列上的数是1，其余都是零的简单形状叫做矩阵的标准形。如4×5阶方阵对角线上a11、a22、a33为1，a44为0、a45以及其他元素都为0的矩阵就是标准形。

任意矩阵都可以用初等变换化为标准形。

4.8、对称矩阵和反对称矩阵

1. 对称矩阵（Symmetric Matrices）是指以主对角线为对称轴，各元素对应相等的矩阵，即矩阵元素aij = aji

2. 对于任何方形矩阵X，X+XT是对称矩阵

3. A为方形矩阵是A为对称矩阵的必要条件

4. 对称矩阵A与其转置矩阵A’相等

5. 设A为n维方阵，若有A’=-A，则称矩阵A为反对称矩阵。对于反对称矩阵，它的主对角线上的元素全为零，而位于主对角线两侧对称的元反号。

4.9、正交矩阵和正交条件

n阶实矩阵A和其转置矩阵A’如果满足：AA’=A’A=E，则n阶实矩阵A称为正交矩阵，正交矩阵通常用字母Q表示。

根据定义可以知道，对于正交矩阵A=(aij),i,j∈[1,n]，则：

1. a²1i+a²2i+…+a²ni = 1

2. a²i1+a²i2+…+a²in = 1

3. 当i≠j时，a1ia1j+a2ia2j+…+ani anj= 0

4. 当i≠j时，ai1aj1+ai2aj2+…+ain ajn= 0

这是正交矩阵元素间的重要性质，也称为正交条件。

如下三个矩阵都是正交矩阵：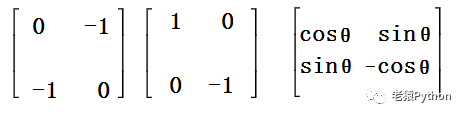

正交矩阵性质：
假设A是正交矩阵，A’是A的转置矩阵，则：

1. A’是正交矩阵

2. A和A’的各行是单位向量且两两正交

3. A和A’的各列是单位向量且两两正交

4. |A|=1或-1，如果正交矩阵的行列式为+1，则称之为特殊正交矩阵

5. A’=A-1,即正交矩阵的转置矩阵与其逆矩阵相等

6. 正交矩阵的逆是正交矩阵，两个正交矩阵的积是正交矩阵、

7. 正交矩阵互换两行或两列还是正交矩阵

4.10、初等矩阵

初等矩阵是指由单位矩阵经过一次初等变换得到的矩阵。初等矩阵的模样可以写一个3阶或者4阶的单位矩阵。

定理：任意矩阵A经过行（列）初等变换成的矩阵等于用初等矩阵左（右）乘A的乘积

五、矩阵的其他概念

• 矩阵等价

• 矩阵等价定义
  加入矩阵A经过有限次初等变换转换为矩阵B，就称A与B等价，表示为：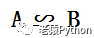
  

定理1：两个矩阵等价的充要条件就是二者的秩相等。

• 自反律：矩阵A和自身等价；

• 对称律：如果A等价于B，则B等价于A；

• 传递律：如果A等价于B，B等价于C，则A等价于C。

定理2：两个矩阵等价的充要条件就是存在两个满秩矩阵P、Q，使得：B = PAQ

定理3：对于矩阵A、B，B是满秩矩阵，那么AB或BA的秩与A的秩相等。

• 如果两个矩阵行数和列数相等则称两个矩阵同型

• 一个矩阵的元全是实数，则该矩阵称为实矩阵

• 矩阵的元都是零的矩阵称为零矩阵

• 把矩阵A的各元变号得到的矩阵，叫做A的负矩阵，用-A表示；

• n阶矩阵A主对角线上n个数的和叫做矩阵A的迹，用tr(A)表示

定理4：矩阵A是满秩矩阵的充要条件是它能够表示为初等矩阵的乘积

六、小结

本文介绍了矩阵的定义、几种特殊矩阵、矩阵的秩等概念，并介绍了矩阵的加法、减法、数乘和乘法运算，由于向量可以看做单行或单列的矩阵，因此矩阵也可以用于向量运算。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》

本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/JliKKdN5ZQb85NkvRXJ0Dg，如有侵权，请联系删除。