编程语言
269
一、红黑树简介
红黑树的规则有
1.每个节点不是红色就是黑色 2.根节点是黑色 3.如果一个节点是红色,它的两个孩子节点是黑色 4.每条路径都有相同数量的黑色节点 5.叶子节点(Nullptr节点)是黑的
这些规则可以推导出红黑树的特性
其最长路径不超过最短路径的两倍,近似平衡 没有连续的红节点 左右子树的黑节点个数相同
其相较于AVL树并没有过多的旋转 用较不平衡换取了性能
在实际中,红黑树的应用相较于AVL树更加常用
二、红黑树的模拟实现
#pragma once #include<iostream> using namespace std; enum Color { Red, Black }; template<class K, class V> struct RBTreeNode { RBTreeNode* _left; RBTreeNode* _right; RBTreeNode* _parent; Color _col; pair<K, V> _kv; RBTreeNode(const pair<K, V>& kv) :_left(nullptr) , _right(nullptr) , _parent(nullptr) , _col(Red) , _kv(kv) {} //定义一个节点时要注意其颜色:不过黑红的地位有所不同,选择决定后续的执行是否简单 //选择红色:违背红色不能连续出现 //选择黑色:违背整体路径黑色数量一致 //红色更好,红色调节节点即可,黑色调节整个路径 }; template<class K, class V> class RBTree { typedef RBTreeNode<K, V> Node; public: bool Insert(const pair<K, V>& kv) { if (_root == nullptr) { _root = new Node(kv); _root->_col = Black; return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; } else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; } else { return false; } } //找到需要插入的位置后 cur = new Node(kv); //默认插入为红色 if (cur->_kv.first > parent->_kv.first) parent->_right = cur; else parent->_left = cur; cur->_parent = parent; //开始处理颜色 while (parent && parent->_col == Red) // { Node* grandpa = parent->_parent; //分两种情况,更方便旋转,父在左 or 父在右 if (grandpa->_left == parent) //父在左 { Node* uncle = grandpa->_right; //情况1:uncle不为空且为红色 //parent和uncle变黑,grandpa变红 //grandpa的父亲为黑,停止 //grandpa的父亲为红,继续向上 if (uncle && uncle->_col == Red) //uncle不为空且为红 { parent->_col = uncle->_col = Black; grandpa->_col = Red; cur = grandpa; grandpa = cur->_parent; } //情况2:uncle为空或者为黑色 else { if (cur == parent->_right) //此时需要双旋 { RotateL(parent); //左旋 swap(parent, cur); //cur和parent进行交换,使得变得和单旋时的条件一样,一举两得 } RotateR(grandpa); parent->_col = Black; grandpa->_col = Red; } break; //处理完直接跳出来 } else //父在右 { Node* uncle = grandpa->_left; if (uncle && uncle->_col == Red) { parent->_col = uncle->_col = Black; grandpa->_col = Red; cur = grandpa; grandpa = cur->_parent; } else { if (cur == parent->_left) //双旋 { RotateR(parent); swap(parent, cur); } RotateL(grandpa); grandpa->_col = Red; parent->_col = Black; } break; } } _root->_col = Black; //确保根节点为黑,流氓方法 return true; } void Print() { _Print(_root); } bool Inspect() { return _Inspect(_root); } private: Node* _root = nullptr; void _Print(Node*& cur) { if (cur == nullptr) return; _Print(cur->_left); cout << cur->_kv.first << " "; _Print(cur->_right); } void RotateL(Node*& parent) { Node* pparent = parent->_parent; Node* subR = parent->_right; Node* subRL = subR->_left; if (pparent == nullptr) { _root = subR; subR->_parent = nullptr; } else { if (pparent->_left == parent) pparent->_left = subR; else pparent->_right = subR; subR->_parent = pparent; } parent->_parent = subR; subR->_left = parent; parent->_right = subRL; if (subRL != nullptr) subRL->_parent = parent; } void RotateR(Node*& parent) { Node* pparent = parent->_parent; Node* subL = parent->_left; Node* subLR = subL->_right; if (pparent == nullptr) { _root = subL; subL->_parent = nullptr; } else { if (pparent->_left == parent) pparent->_left = subL; else pparent->_right = subL; subL->_parent = pparent; } parent->_parent = subL; subL->_right = parent; parent->_left = subLR; if (subLR != nullptr) subLR->_parent = parent; } bool check(Node* root, size_t& reference, size_t num) { if (root == nullptr) { if (num != reference) { cout << "路径长度有问题" << endl; return false; } return true; } if (root->_col == Red && root->_parent && root->_parent->_col == Red) { cout << "节点连续红色" << endl; return false; } if (root->_col == Black) num++; return check(root->_left, reference, num) && check(root->_right, reference, num); } bool _Inspect(Node* root) { //空树也是红黑树 if (_root == nullptr) return true; //检测根节点是否为黑色 if (_root->_col != Black) { cout << "根节点是红色的" << endl; return false; } size_t leftNum = 0; Node* cur = _root; while (cur) { if (cur->_col == Black) leftNum++; cur = cur->_left; } //检测所有路径黑色节点的数量是否一样 //检测相邻节点是不是都是红色的 return check(_root, leftNum, 0); } };
三、双红色问题解决原理图
1.叔父同色

2.叔不存在或为黑,单旋
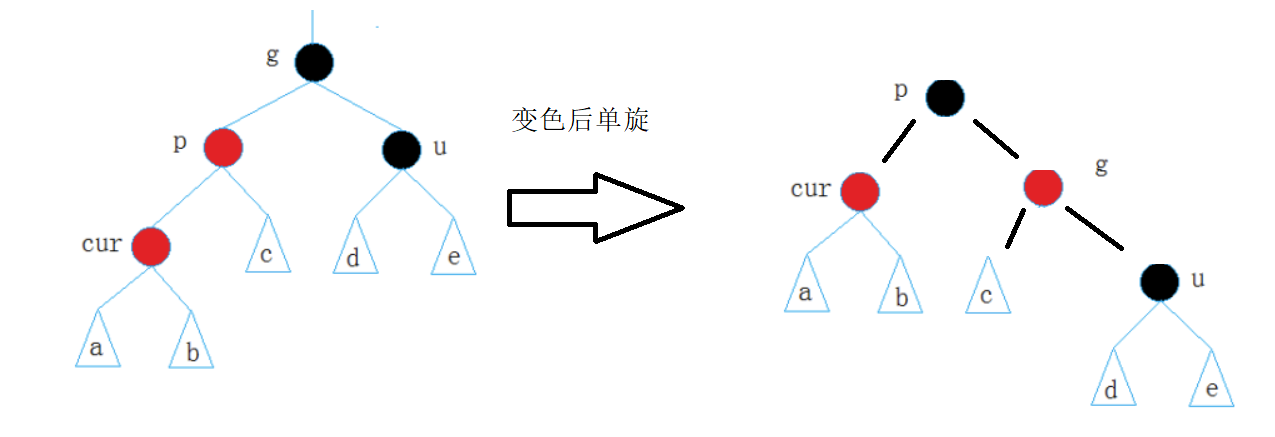
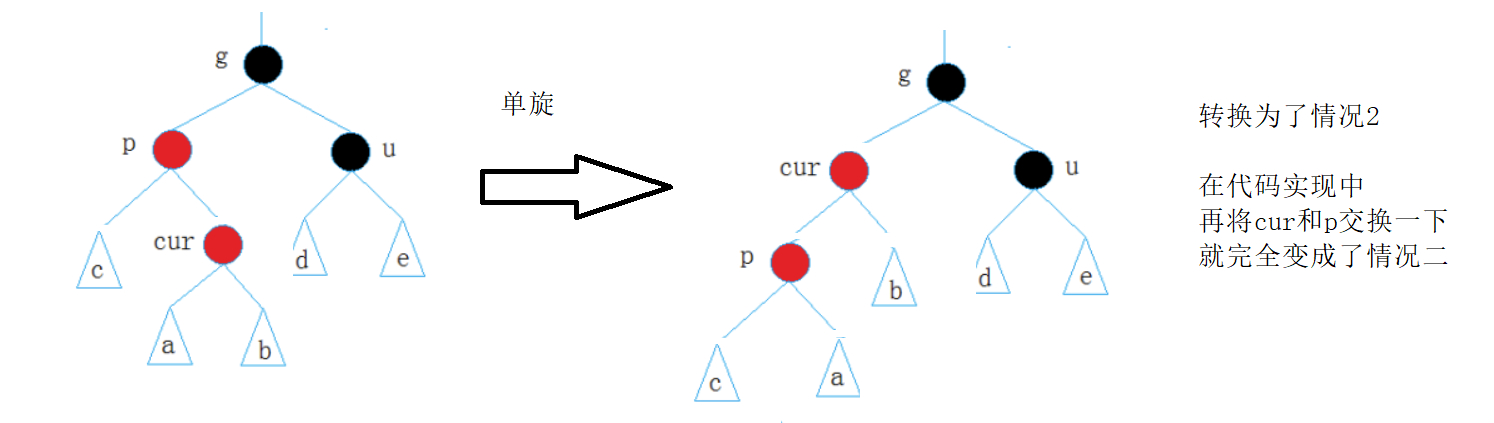
3.叔不存在或为黑,双旋
广告











