编程语言
1070
一、模拟实现AVL树
AVL树就是高度平衡二叉搜索树 所有树的左右子树高度差不超过1 平衡因子 = 右子树高度 - 左子树高度
#pragma once #include<iostream> #include<assert.h> using namespace std; template<class K,class V> struct AVLTreeNode { AVLTreeNode<K, V>* _left; AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent; //三叉链 int _bf; //平衡因子 balance factor pair<K, V> _kv; AVLTreeNode(const pair<K, V>& kv) :_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_bf(0) ,_kv(kv) {} }; template<class K,class V> class AVLTree { typedef AVLTreeNode<K, V> Node; public: bool Insert(const pair<K,V>& kv) { if (_root == nullptr) { _root = new Node(kv); return true; } Node* parent = nullptr; Node* cur = _root; while (cur!=nullptr) { if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; } else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; } else { return false; } } cur = new Node(kv); //开始连接 if (cur->_kv.first > parent->_kv.first) { parent->_right = cur; cur->_parent = parent; } else { parent->_left = cur; cur->_parent = parent; } //1.cur是parent的左,parent->_bf--,是右则++; //2.更新后的_bf如果是0,说明parent高度没有发生变化 : 更新前_bf为 -1/1 ,变为0说明把矮的那边填上 //3.更新后的_bf为-1/1,说明parent变高了,继续向上更新 //4.更新后的_bf为-2/2,说明parent的子树出现了不平衡,需要进行旋转处理 //开始更新平衡因子 while (parent) { if (cur == parent->_right) parent->_bf++; else parent->_bf--; if (parent->_bf == 0) break; //parent所在的子树高度没有变化,更新结束 else if (parent->_bf == 1 || parent->_bf == -1) { //parent所在的子树变高了,需要继续向上进行更新 cur = parent; parent = parent->_parent; } else if (parent->_bf == 2 || parent->_bf == -2) { //parent所在的子树出现了不平衡,需要旋转更新 //右重,向左压,左单旋 if (parent->_bf == 2 && cur->_bf == 1) RotateL(parent); //左重,向右压,右单旋 else if (parent->_bf == -2 && cur->_bf == -1) RotateR(parent); //头右重,左重,右左双旋 else if (parent->_bf == 2 && cur->_bf == -1) RotateRL(parent); //头左重,右重,左右双旋 else if (parent->_bf == -2 && cur->_bf == 1) RotateLR(parent); else assert(false); break; } else assert(false); } } void RotateL(Node*& parent) //左旋,\ 右重 { Node* subR = parent->_right; Node* subRL = subR->_left; Node* ppNode = parent->_parent; subR->_left = parent; parent->_right = subRL; parent->_parent = subR; if (subRL != nullptr) //当其为空时不用赋值,且赋值时会访问错误 : nullptr->_parent { subRL->_parent = parent; } if (ppNode == nullptr) //parent就是根 { _root = subR; subR->_parent = nullptr; } else //parent是子树 { if (ppNode->_left == parent) ppNode->_left = subR; else ppNode->_right = subR; subR->_parent = ppNode; } parent->_bf = 0; subR->_bf = 0; } void RotateR(Node*& parent) //右旋,/ 左重 { Node* subL = parent->_left; Node* subLR = subL->_right; Node* ppNode = parent->_parent; if (ppNode == nullptr) { _root = subL; subL->_parent = nullptr; } else { if (ppNode->_left == parent) ppNode->_left = subL; else ppNode->_right = subL; subL->_parent = ppNode; } if (subLR != nullptr) { subLR->_parent = parent; } parent->_left = subLR; parent->_parent = subL; subL->_right = parent; parent->_bf = 0; subL->_bf = 0; } void RotateRL(Node*& parent) //先右单旋再左单旋 \ // /\; { Node* subR = parent->_right; Node* subRL = subR->_left; int tmp_bf = 0; if (subRL->_left == nullptr && subRL->_right == nullptr) //subRL无子树时,其他树也无子树,相当于只有三棵树 { tmp_bf = 0; } else { tmp_bf = subRL->_bf; //通过判断tmp_bf大小来对旋转后的各树_bf进行不一样的赋值方式 } RotateR(subR); //注意传入的参数 RotateL(parent); if (tmp_bf == 0) { parent->_bf = 0; subR->_bf = 0; } else if(tmp_bf == 1) { parent->_bf = -1; subR->_bf = 0; } else if (tmp_bf == -1) { parent->_bf = 0; subR->_bf = 1; } subRL->_bf = 0; } void RotateLR(Node*& parent)//先左单旋再右单旋 / // /\; { Node* subL = parent->_left; Node* subLR = subL->_right; int tmp_bf = 0; if (subLR->_left == nullptr && subLR->_right == nullptr) tmp_bf = 0; else tmp_bf = subLR->_bf; RotateL(subL); RotateR(parent); if (tmp_bf == 0) { subL->_bf = 0; parent->_bf = 0; } else if (tmp_bf == 1) { subL->_bf = -1; parent->_bf = 0; } else if(tmp_bf == -1) { subL->_bf = 0; parent->_bf = 1; } subLR->_bf = 0; } void Print() { _Print(_root); } void _Print(Node*& cur) { if (cur == nullptr) return; _Print(cur->_left); cout << cur->_kv.first << ":" << cur->_kv.second << endl; _Print(cur->_right); } int Height(Node* root) { if (root == nullptr) return 0; int left = 1 + Height(root->_left); int right = 1 + Height(root->_right); return left > right ? left : right; } bool Check() { return _Check(_root); } bool _Check(Node* root) { if (root == nullptr) return true; int leftHeight = Height(root->_left); int rightHeight = Height(root->_right); int dif = rightHeight - leftHeight; if (dif != root->_bf) { cout << "No" << endl; return false; } if (abs(dif) > 1) { cout << "Not" << endl; return false; } return _Check(root->_left) && _Check(root->_right); } private: Node* _root = nullptr; };
二、旋转原理图
1.右单旋原理图

2.左单旋原理图
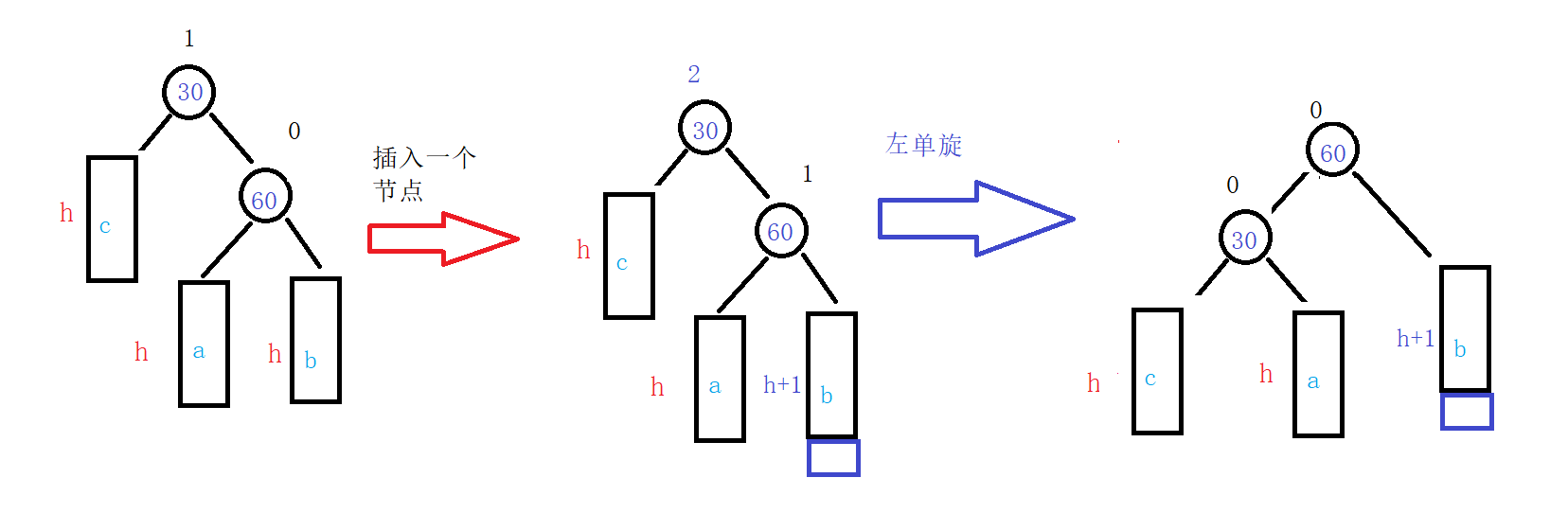
3.右左双旋

4.左右双旋











